Indefinite and Definite Integrals
We want to find the indefinite integral of one of the usual textbook examples, e.g.:
> f := x^2*sin(x)*exp(-3*x);
![]()
> int(f, x);
![]()
To test the result, we differentiate it:
> diff(%,x);
![]()
![]()
> simplify(%);
![]()
Next we try a rational function:
> g := (2*x^2-3*x+1)/(x^5-7*x^4+17*x^3-19*x^2+16*x-12);
![[Maple Math]](images/m36.gif)
> int(g, x);
![]()
To see what Maple did, we look at the partial fraction decomposition:
> factor(g);
![[Maple Math]](images/m38.gif)
> convert(g, parfrac, x);
![[Maple Math]](images/m39.gif)
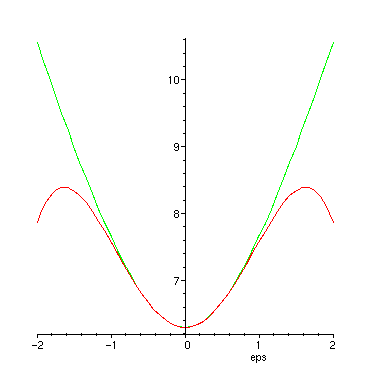
Finally we want to compute the circumference of an ellipse of excentricity eps:
The parameter form of the ellipse leads to the following integral for the circumference:
> f1 := sqrt(1+eps^2*sin(t)^2);
![]()
> l_ell := 4*int(f1, t=0..Pi/2);
![]()
The integral can not be solved with the usual functions. Since it appears in many different contexts, one has given a special name to it: "complete elliptic integral of the second kind". We look at its taylor expansion and function graph:
> taylor(%, eps=0, 5);
![]()
For the plot of the approximation we have to throw away the O(..) term:
> l_approx := convert(%, polynom);
![]()
> plot({l_ell,l_approx}, eps=-2..2);